“Funzione” è più facile di “formula”, meno spavento, però . . .

È un’idea, e una parola, che sono emerse un po’ alla volta, alla fine di una serie di slittamenti di significato, quelli che nell’evoluzione temporale delle lingue sono così frequenti, ancorché imprevedibili, cui anche la matematica stessa ha contribuito. Il punto di partenza sembra essere il verbo latino fungor, il quale originariamente indica l’adempiere un dovere, il ricoprire una mansione: consulatu fungi significa, per i latini di età classica, “esercitare il consolato”.

A. Primo passo: da qui segue che si può usare la parola per dire che si esercita una mansione di un altro, se ne ricopre il ruolo, tipicamente, sempre nel latino classico, fungi maternis vicibus significa “far le veci della madre”. Da questa direzione di significati deriva l’italiano fungere che incorpora già ‘le veci’, “fungere da sostegno” sta per “fare quello che fa un sostegno”, anche se lo scopo originario non era quello, “fungere da madre” significa esercitare le mansioni della madre pur non essendo la madre, si può equivalentemente anche dire “fare la funzione di un sostegno”, o “della madre”, rispettivamente. Dunque la parola funzione indica qui un passaggio di azione da una cosa ad un’altra, o da una persona ad un’altra, una sostituzione, un prender su di sé la figura di qualcos’altro. Secondo la Costituzione italiana nel caso di impedimento del Capo dello Stato, il presidente del Senato ne assume le funzioni (in questo momento sarebbe una vera iattura): vuol dire che egli, pur non essendo il capo dello stato eletto, ne assume il ruolo, prende su di sé l’onere – e l’onore – della carica.

B. Secondo passo: a questo punto si è verificato un nuovo, e fondamentale, spostamento di significato all’interno della storia della matematica, a partire dagli ultimi decenni del secolo XVII. Descrivere, seppur in modo molto schematico, questo frammento di storia della matematica ci permetterà di cogliere un’altra istanza di quella dicotomia estensione/intensione così frequente nella logica (e cui spesso si dedica troppo scarsa attenzione). In una prima fase, che si può far simbolicamente coincidere con l’opera di Newton (ricordate che i suoi Principia sono del 1687), l’idea che una qualche grandezza possa dipendere da un’altra, possa cioè variare al variare di un’altra, è limitata al caso in cui quest’ultima grandezza sia il tempo; Newton non usa ancora la parola funzione, ma usa la parola latina fluentes per indicare queste entità che hanno la caratteristica di cambiare col tempo. La parola funzione, o per meglio dire la sua versione latina functio, appare per la prima volta nella storia della matematica in un manoscritto di Leibniz del 1673 intitolato Methodus tangentium inversa, seu de functionibus, nel quale ancora si parla del calcolo di certe speciali caratteristiche di una curva piana (quali la sottotangente, la sottonormale e altre, che qui poco importano), che rivestono un certo ruolo nell’andamento della curva, e dunque ancora la parola rimane nell’alveo del significato di ‘ruolo’. Leibniz si serve invece per indicare la dipendenza dell’ordinata di un punto della curva dalla sua ascissa, della parola relatio, ‘relazione’. Ma nel prosieguo del manoscritto, ecco che l’autore si serve della parola functio per indicare appunto in generale come queste varie caratteristiche della curva variano lungo di essa, in quanto il suo scopo, nel manoscritto, è quello di risalire dal variare di queste caratteristiche alla forma della curva – di ricavare dalle functiones la relatio; nello stesso senso allargato Leibniz continuerà ad usare la parola in altri lavori del 1692 e del 1694.

C. Terza tappa. Occorre guardare a un personaggio chiave immediatamente successivo a Leibniz, il matematico e fisico svizzero Johann Bernoulli (Basilea 1667-1748), maestro di Eulero. È a lui che si deve la prima definizione formale di che cosa sia una funzione in quanto quantità composta di grandezze variabili:

Définition. On appelle fonction d’une grandeur variable une quantité composée de quelque manière que ce soit de cette grandeur variable et de constants.

L’aspetto interessante di questa definizione, oltre a quello di essere un primo tentativo di formalizzare la parola funzione all’interno delle matematiche, è quello di identificare una funzione con una espressione formale. Ad esempio x² ; (3x)ⁿ-x³ ; (x-1)/(x+1) ; (purché nella terza espressione, si intenda x ≠ −1, altrimenti perde senso l’espressione, uno zero non può stare al denominatore) sono tutte espressioni legittime, o, meglio, ben formate. Dunque, in questa prima fase della ricerca di cosa è funzione, si adotta un atteggiamento tipicamente connotativo, intensivo: per assegnare una funzione occorre che sia data una espressione che permetta di calcolarla. Essa non è certamente unica, ad esempio le espressioni (x − 1)(x + 1) e x² − 1, chiaramente diverse in quanto espressioni, danno luogo agli stessi valori: per x = 2 forniscono entrambe il valore 3, per x = −1 danno entrambe il valore 0 e lo stesso accade per qualsiasi altro valore attribuito alla x; ma si vede allora che, secondo la definizione di Bernoulli esse sono funzioni diverse, in quanto composizioni di simboli diverse; tuttavia si vorrebbe in maniera naturale identificarle in quanto portano appunto agli stessi numeri a partire dagli stessi numeri. Questo spinge ad adottare una definizione di funzione che badi non tanto alla sua espressione formale, ma al risultato che si ottiene per ogni valore della variabile.

D. Quarta tappa. Già nel XVIII, e poi più decisamente nel XIX secolo comincia ad affermarsi la tendenza a generalizzare la definizione di funzione, svincolandola dall’esigenza di una sua rappresentazione analitica; la prima vera formulazione di questo tipo è dovuta a Eulero (Leonhard Euler, Basilea 1707 – San Pietroburgo 1783, che molto profitto aveva tratto dagli insegnamenti di Bernoulli) e suona così:

Se alcune quantità dipendono da altre quantità in modo tale che se queste ultime vengono cambiate allora le prime anche cambiano, allora queste sono dette funzioni delle seconde. Questa denominazione è della più ampia natura e comprende ogni metodo per mezzo del quale una quantità può esser determinata da altre. Se perciò x denota una quantità variabile allora tutte le quantità che dipendono dalla x in un qualsiasi modo, o sono da questa determinate, sono dette funzioni di x.

Quest’idea non fu immediatamente condivisa dai matematici europei, ma dopo qualche decennio cominciò ad affermarsi definitivamente, nelle opere di Lagrange, Lacroix, Fourier e – infine – di Lobačevskij e Dirichlet. Da questi pur rapidissimi cenni storici si dovrebbe poter dedurre almeno che l’idea che sta alla base del concetto di funzione è quella di dipendenza di una grandezza da un’altra, o da varie altre. Si noti tuttavia che la parola ‘dipendenza’ può alludere – connotativamente – ad un modo causale formalmente esprimibile nel quale una grandezza y è determinata da un’altra grandezza x – la direzione di marcia di un’auto dipende strettamente dai movimenti dello sterzo – oppure questa dipendenza può essere più astratta e casuale: provate a pensare di associare ad ogni intervallo di un minuto della notte dal 10 all’11 agosto 2022 il numero di stelle cadenti visibile a occhio nudo in un fissato quadrante del cielo boreale: è chiaro che anche questa funzione è perfettamente definita e determinata, ma è molto meno chiaro come si possa in qualche modo risalire dal valore della variabile indipendente (l’intervallo di un minuto) a quello della funzione (il numero di stelle cadenti in quel minuto), se non mediante una accurata osservazione. È chiaro che in quest’ultimo caso la funzione è data in modo squisitamente estensivo: si osserva – e si trascrive poi eventualmente in un grafico – il valore corrispondente ad ogni minuto; mentre nel caso dello sterzo c’è sicuramente modo di calcolare – e quindi anticipare – la direzione di marcia in termini dell’angolo di rotazione dello sterzo.

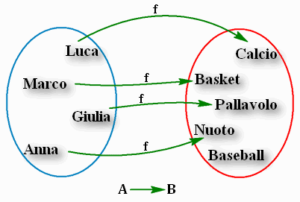
Concludiamo per il momento che in matematica la parola ha assunto un significato diverso da quello che ha nella lingua comune, nella quale, ad esempio, le funzioni di una persona, o di una macchina sono ciò che questa persona, o macchina deve fare per assolvere i suoi compiti; siamo ancora alla fine del passo A di cui sopra. Nella figura che vedete all’inizio la funzione associa ad ognuno dei quattro, ragazze e ragazzi, il suo sport preferito, scelto in un altro insieme, quello degli sport, che non tutto deve necessariamente essere “coperto” dalla funzione in questione. Ma credo che tornerò sul ruolo delle funzioni nel linguaggio scientifico.