L’idea di funzione #2
di Antonio Sparzani
Ed eccoci – dopo quanto visto qui – all’ultimo passo del cammino che porta a una definizione di funzione che finalmente ci soddisferà.
D. Quarto passo. Già nel XVIII, e poi più decisamente nel XIX secolo comincia ad affermarsi la tendenza a generalizzare la definizione di funzione, svincolandola dall’esigenza di una sua rappresentazione analitica, cioè dalla necessità – formale – di rappresentarla con una formula; la prima vera formulazione di questo tipo è dovuta a Eulero 1 e suona così:
«Se alcune quantità dipendono da altre quantità in modo tale che se queste ultime vengono cambiate allora le prime anche cambiano, allora queste sono dette funzioni delle seconde. Questa denominazione è della più ampia natura e comprende ogni metodo per mezzo del quale una quantità può esser determinata da altre. Se perciò x denota una quantità variabile allora tutte le quantità che dipendono dalla x in un qualsiasi modo, o sono da questa determinate, sono dette funzioni di x.
Quest’idea non fu immediatamente condivisa dai matematici europei, ma dopo qualche decennio cominciò ad affermarsi definitivamente, nelle opere di Lagrange, Lacroix, Fourier e – infine – di Lobačevskij e Dirichlet.
Questi schematici accenni dovrebbero suggerire che l’idea che sta alla base del concetto di funzione è quella di dipendenza di una grandezza da un’altra, o da varie altre. Notate però che la parola ‘dipendenza’ può alludere a due situazioni differenti: la prima – connotativa – ad un modo causale formalmente esprimibile nel quale una grandezza y è determinata da un’altra grandezza x , esempio: la direzione di marcia di un’auto dipende strettamente dai movimenti dello sterzo; la seconda – denotativa – e dunque più astratta e casuale – esempio: se associate ad ogni intervallo di un minuto della notte dal 10 all’11 agosto 2014 il numero di stelle cadenti visibile a occhio nudo in un fissato quadrante del cielo boreale, è chiaro che ottenete una funzione perfettamente definita e determinata, ma è molto meno chiaro come si possa in qualche modo risalire dal valore della variabile indipendente (il generico intervallo di un minuto) a quello della funzione (il numero di stelle cadenti apparse in quel minuto), l’unico modo è quello di una accurata osservazione. È chiaro che in questo caso la funzione è data in modo squisitamente estensivo: si osserva – e si trascrive poi eventualmente in un grafico – il valore corrispondente ad ogni minuto; mentre nell’esempio dello sterzo c’è sicuramente modo di calcolare – e quindi anticipare – la direzione di marcia in termini dell’angolo di rotazione dello sterzo.
Allora la funzione c’è quando una cosa dipende da un’altra: al variare di questa varia quella, in un qualche modo che può essere il più vario possibile. Si tratta di metter tutto questo in una forma razionalmente corretta e comprensibile. Per farlo occorre che nella definizione sia contenuta da un lato la presenza di una quantità che può variare (e che sarà detta variabile indipendente) all’interno di un certo ben precisato ambito di possibilità – e che è detto dominio della funzione – e dall’altro la descrizione di un ambito, in generale diverso dal primo – detto codominio, o anche range, della funzione – in cui può variare la quantità (detta variabile dipendente) che dipende dalla prima; oltre a ciò occorre che sia esattamente precisata questa dipendenza. Come s’è detto questa “precisazione” può essere formale – analitica, cioè esprimibile con formule – o invece fornita dall’osservazione dei fatti. Nell’idea di funzione c’è dunque qualcosa di profondamente non simmetrico, c’è una grandezza che varia arbitrariamente all’interno di un certo ambito e ce n’è poi un’altra che varia al variare della prima. Questa non simmetria si evidenzia anche da questa caratteristica di ogni funzione, che viene detta la sua univocità: dato un valore della variabile indipendente, dunque appartenente al suo dominio, uno e un solo valore della variabile dipendente gli corrisponde. Per ogni valore dell’età di Alice è univocamente determinata la sua altezza: ad una determinata età Alice non può avere due altezze diverse. Ma se invece fissate un valore dell’altezza (dunque del codominio della funzione che stiamo considerando) esisteranno certamente molti valori dell’età di Alice cui quel valore corrisponde: Alice non continua a crescere per tutta la sua vita, né a decrescere.
Un modo standard usato dai matematici pignoli per scrivere tutto questo è questo:
Dove D indica il dominio della funzione f , W indica il codominio, x il generico elemento di D e le freccette alludono in qualche modo alla asimmetria della situazione.
- Leonhard Euler (Basilea 1707 – San Pietroburgo 1783), grande matematico e fisico svizzero; fu allievo di Johann Bernoulli, e succedette nel 1733 al figlio di questi, Daniel, sulla cattedra di matematica dell’Accademia di San Pietroburgo. Scrisse la definizione qui riportata nella prefazione delle sue Institutiones calculi differentialis, pubblicate nel 1755.↩
I commenti a questo post sono chiusi


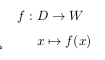

Grazie Sparz! Siamo un po’ troppo abituati a usare concetti dei quali ci sfugge l’estensione e il significato.